全国2017年10月自考线性代数(经管类)真题
温馨提示
亲爱的学员,您好!
全国2017年10月高等教育自学考试线性代数(经管类)试题
课程代码:04184
请考生按规定用笔将所有试题的答案涂、写在答题纸上。
说明:在本卷中,AT表示矩阵A的转置矩阵,A*表示矩阵4的伴随矩阵,E是单位矩阵,|A|表示方阵A的行列式,r(A)表示矩阵A的秩。
选择题部分
注意事项:
1.答题前,考生务必将自己的考试课程名称、姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸规定的位置上。
2.每小题选出答案后,用2B铅笔把答题纸上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。不能答在试题卷上。
一、单项选择题:本大题共5小题,每小题2分,共10分。在每小题列出的备选项中只有一项是最符合题目要求的,请将其选出。
1.设A,B是n阶可逆矩阵,下列等式中正确的是
A. (A+B)-1 =A-1 +B-l B.(AB)-1=A-1B-1
C. (A-B)-1 =A-l-B-1 D. (AB)-1=B-1A-1
2.设A为3阶矩阵且r(A)=l,B= 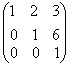 ,则r(BA)=
,则r(BA)=
A. 0 B. 1 C. 2 D. 3
3.设向量组α1=(1,2,3),α2=(0,l,2),α3=(0,0,l),β=(1,3,6),则
A. α1,α2,α3,β线性无关
B. β不能由α1,α2,α3线性表示
C. β可由α1,α2,α3线性表示,且表示法惟一
D. β可由α1,α2,α3线性表示,但表示法不惟一
4.设A为4×5矩阵且r(A)=4,则齐次线性方程组Ax=0的基础解系中所含向量的个数为
A. 1 B. 2 C. 3 D. 4
5.设3阶矩阵A的特征多项式为|λE-A|=(λ-2)(λ+3)2,则|A+E| =
A. -18 B. -12 C. 12 D. 18
非选择题部分
注意事项:用黑色字迹的签字笔或钢笔将答案写在答题纸上,不能答在试题卷上。
二、填空题:本大题共10小题,每小题2分,共20分。
6.行列式 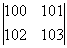 的值为________.
的值为________.
7.设A为3阶矩阵,|A|=1,则|-2A|=________.
8.设n阶矩阵A的所有元素都是1,则r(A)=________.
9.设A为3阶矩阵,将A的第1行与第2行交换得到矩阵B,则|A-B|=________.
10.设 3 维向量α=(3,-1,2)T,β=(3,1,4)T ,若向量γ满足2α+γ=3β ,则γ=________.
11.已知线性方程组 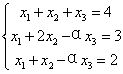 无解,则数α=________.
无解,则数α=________.
12.设向量α=(1,1,3),β=(1,-1,1),矩阵A=αTβ,则矩阵A的非零特征值为________.
13.已知3阶矩阵A的特征值为1,2,3,且矩阵B与A相似,则|B2+E|=________.
14.已知向量组α1=(l,2,3),α2=(2,2,k)正交,则数k=________.
15.已知3阶实对称矩阵A的特征多项式|λE-A| =(λ-l)(λ+2)(λ-5),则二次型ƒ(x1,x2,x3)=xTAx的正惯性指数为________.
三、计算题:本大题共7小题,每小题9分,共63分。
16.计算4阶行列式 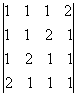 的值。
的值。
17.已知矩阵A=(2,1,0),B=(1,2,3),ƒ(x)= x2-5x + 1,求ATB及ƒ(ATB)。
18.已知矩阵A,B满足AX=B,其中A= 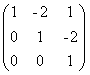 ,B=
,B= 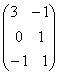 ,求X.
,求X.
19.求向量组α1=(1,1,1,0)T,α2=(-1,-3,5,4)T,α3=(2,1,-2,-2)T,α4=(-1,-5,11,8)的一个极大线性无关组,并将向量组中的其余向量用该极大线性无关组线性表出。
20.设3元齐次线性方程组 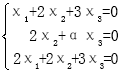 ,确定α为何值时,方程组有非零解,并求其通解。
,确定α为何值时,方程组有非零解,并求其通解。
21.设矩阵A= 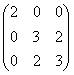 ,求可逆矩阵P和对角矩阵Λ,使得P-1AP=Λ。
,求可逆矩阵P和对角矩阵Λ,使得P-1AP=Λ。
22.已知ƒ(x1,x2,x3)=x12+4x22+2x32+2tx1x2-2x1x3为正定二次型,(1)确定t的取值范围;(2)写出二次型ƒ(x1,x2,x3)的规范形。
四、证明题:本题7分。
23.证明矩阵A= 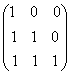 不能对角化。
不能对角化。
《广东自考网》免责声明:
1、由于考试政策等各方面情况的调整与变化,本网提供的考试信息仅供参考,最终考试信息请以省考试院及院校官方发布的信息为准。
2、本站内容部分信息均来源网络收集整理或来源出处标注为其它媒体的稿件转载,免费转载出于非商业性学习目的,版权归原作者所有,如有内容与版权问题等请与本站联系。联系邮箱:812379481@qq.com


















